量化分析师的 Python 日记 [Q Quant 之初出江湖]

[datayes2015]

本篇中，作为 Quant 中的 Q 宗（ P Quant 和 Q Quant 到底哪个是未来？)，我们将尝试把之前的介绍的工具串联起来，小试牛刀。

您将可以体验到： https://uqer.io/community/share/5514fc98f9f06c8f33904449

如何使用 python 内置的数学函数计算期权的价格；
利用 numpy 加速数值计算；
利用 scipy 进行仿真模拟；
使用 scipy 求解器计算隐含波动率；
穿插着，我们也会使用 matplotlib 绘制精美的图标。
1. 关心的问题 https://uqer.io/community/share/5514fc98f9f06c8f33904449

我们想知道下面的一只期权的价格：

当前价 spot : 2.45
行权价 strike : 2.50
到期期限 maturity : 0.25
无风险利率 r : 0.05
波动率 vol : 0.25
关于这样的简单欧式期权的定价，有经典的 Black - Scholes [1] 公式：


Call(S,K,r,τ,σ)d1d2= SN(d1)−Ke−rτN(d2),=ln(S/K)+(r+12σ2)τστ√,=d1−στ√.
其中 S 为标的价格， K 为执行价格， r 为无风险利率，τ=T−t 为剩余到期时间。 N(x)为标准正态分布的累积概率密度函数。 Call(S,K,r,τ,σ)为看涨期权的价格。
https://uqer.io/community/share/5514fc98f9f06c8f33904449
观察上面的公式，需要使用一些数学函数，我们把它分为两部分：

log,sqrt,exp ，这三个函数我们可以从标准库 math 中找到
标准正态分布的累计概率密度函数，我们使用 scipy 库中的 stats.norm.cdf 函数

我们可以使用这个函数计算我们关注期权的结果： https://uqer.io/community/share/5514fc98f9f06c8f33904449

2. 使用 numpy 加速批量计算 https://uqer.io/community/share/5514fc98f9f06c8f33904449

大部分的时候，我们不止关心一个期权的价格，而是关心一个组合（成千上万）的期权。我们想知道， 随着期权组合数量的增长，我们计算时间的增长会有多块？

2.1 使用循环的方式 https://uqer.io/community/share/5514fc98f9f06c8f33904449

从下图中可以看出，计算时间的增长可以说是随着组合规模的增长线性上升。

https://uqer.io/community/share/5514fc98f9f06c8f33904449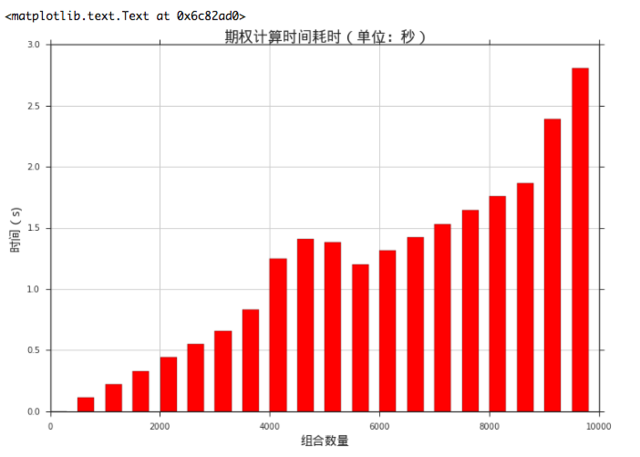


2.2 使用 numpy 向量计算

numpy 的内置数学函数可以天然的运用于向量：
利用 numpy 的数学函数，我们可以重写原先的计算公式 call_option_pricer ，使得它接受向量参数。
再观察一下计算耗时，虽然时间仍然是随着规模的增长线性上升，但是增长的速度要慢许多：


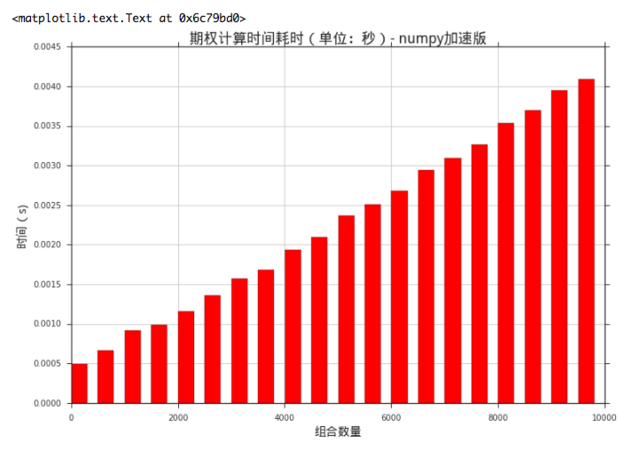
让我们把两次计算时间进行比对，更清楚的了解 numpy 计算效率的提升！


3. 使用 scipy 做仿真计算

期权价格的计算方法中有一类称为 蒙特卡洛 方法。这是利用随机抽样的方法，模拟标的股票价格随机游走，计算期权价格（未来的期望）。假设股票价格满足以下的随机游走：


dS=rSdt+σSdW(t).
仿真的方法可以模拟到期日的股票价格


ST=S0exp((r−12σ2)T+zσT ‾‾√)
这里的 z 是一个符合标准正态分布的随机数。这样我们可以计算最后的期权价格：


price=exp(−rT)∑i=1Nmax(ST,i−K,0)
标准正态分布的随机数获取，可以方便的求助于 scipy 库：


结合 scipy numpy 我们可以定义基于蒙特卡洛的期权定价算法。
我们这里实验从 1000 次模拟到 50000 次模拟的结果，每次同样次数的模拟运行 100 遍。
蒙特卡洛方法会有收敛速度的考量。这里我们可以看到随着模拟次数的上升，仿真结果的置信区间也在逐渐收敛。
4. 计算隐含波动率 https://uqer.io/community/share/5514fc98f9f06c8f33904449

作为 BSM 期权定价最重要的参数，波动率σ是标的资产本身的波动率。是我们更关心的是当时的报价所反映的市场对波动率的估计，这个估计的波动率称为隐含波动率（ Implied Volatility ）。这里的过程实际上是在 BSM 公式中，假设另外 4 个参数确定，期权价格已知，反解σ:

f(σ)=Call(S,K,r,τ,σ)=SN(d1)−Ke−rτN(d2),IF f(σ)=V,Then σ=f−1(V) ?
由于对于欧式看涨期权而言，其价格为对应波动率的单调递增函数，所以这个求解过程是稳定可行的。一般来说我们可以类似于试错法来实现。在 scipy 中已经有很多高效的算法可以为我们所用，例如 Brent 算法:https://uqer.io/community/share/5514fc98f9f06c8f33904449

参考文献

[1] Black, Fischer; Scholes, Myron. The Pricing of Options and Corporate Liabilities. Journal of Political Economy 81 (3): 637 – 654.