前言
梯度下降法( Gradient Descent )是机器学习中最常用的优化方法之一,常用来求解目标函数的极值。
其基本原理非常简单:沿着目标函数梯度下降的方向搜索极小值(也可以沿着梯度上升的方向搜索极大值)。
假设需要求解目标函数是 func(x) = x * x 的极小值,由于 func 是一个凸函数,因此它唯一的极小值同时也是它的最小值,其一阶导函数 为 dfunc(x) = 2 * x 。
import numpy as np
import matplotlib.pyplot as plt
# 目标函数:y=x^2
def func(x):
return np.square(x)
# 目标函数一阶导数:dy/dx=2*x
def dfunc(x):
return 2 * x
梯度下降法函数:
实盘回测代码请移步:
https://uqer.io/community/share/58204a27228e5ba8f85715a8假设起始搜索点为-5 ,迭代周期为 5 ,学习率为 0.3 :
实盘回测代码请移步:
https://uqer.io/community/share/58204a27228e5ba8f85715a8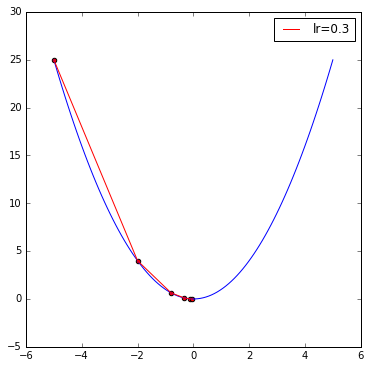
从运行结果来看,当学习率为 0.3 的时候,迭代 5 个周期似乎便能得到较理想的效果。
学习率对梯度下降法的影响
设置学习率分别为 0.1 、 0.3 与 0.9 进行测试:
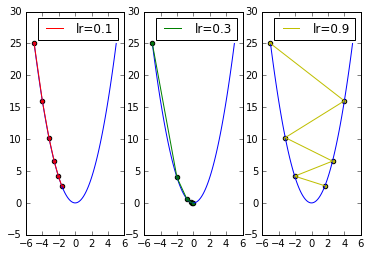
从下图输出结果可以看出两点,在迭代周期不变的情况下:
学习率较小时,收敛到正确结果的速度较慢。
学习率较大时,容易在搜索过程中发生震荡。
学习率大小对梯度下降法的搜索过程起着非常大的影响!
这是一个专为移动设备优化的页面(即为了让你能够在 Google 搜索结果里秒开这个页面),如果你希望参与 V2EX 社区的讨论,你可以继续到 V2EX 上打开本讨论主题的完整版本。
https://www.v2ex.com/t/324299
V2EX 是创意工作者们的社区,是一个分享自己正在做的有趣事物、交流想法,可以遇见新朋友甚至新机会的地方。
V2EX is a community of developers, designers and creative people.

