询问一些入门级的线性代数知识，求解惑

大学时没学好，毕业后这么多年忘光了，最近工作用到，看了一些线性代数书，百度搜了半天，感觉有很多说法互相矛盾，搞不太懂了来问问。

问题 1：矩阵是 m*n ，向量是 k 维的，类似 1*k ，如此看来，认为矩阵由向量组成，这个说法没错吧？我还记得上学的时候还有个叫行列式的东西，这个又是什么？

问题 2：我记得有点乘和叉乘的区别，如下这张图代表的是点乘还是叉乘的计算方法，还是什么其他的别的？

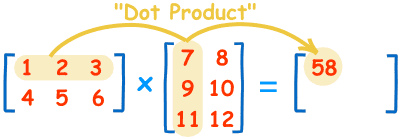
问题 3：接续 2 ，向量的点乘和叉乘，与矩阵的点乘和叉乘是否遵循不同的计算逻辑？

问题 4：numpy 中如下代码：

import numpy as np 
arr1 = np.array([
	[1,2],
	[3,4]
])
arr2 = np.array([
	[5,6],
	[7,8]
])
print(arr1.dot(arr2))

得到的结果是

[[19 22]
 [43 50]]

这个是由点乘还是叉乘算出来的？怎么感觉和上图中显示的计算方式不对呢？如果是叉乘的话又为什么叫 dot 呢，dot 不是点么

问题 5：矩阵中挨个位置直接相乘，比如 2*2 矩阵 1,2,3,4 和 5,6,7,8 相乘，得到 5,12,21,32 的话，这种计算规则是叫什么？

比较基础，大家轻喷。

GuuJiang

2021-11-12 15:17:16 +08:00

1. 没问题，m*n 矩阵可以认为由 m 个行向量组成，也可以认为由 n 个列向量组成，至于行列式。。。还是建议回去翻书吧，这个实在太基础了
2. 点乘和叉乘值得是向量之间的乘法，有的地方把通常意义上的矩阵乘法也叫做点乘，至于你发的这个图，应该是在展示矩阵乘法的其中一个步骤，即 A*B 中的元素[i,j]等于 A 中的第 i 个行向量与 B 中的第 j 个列向量的点积，这也解释了为什么把矩阵乘法也叫做点乘
3. 同上，不存在矩阵的叉乘
4. 同上
5. element-wise product ，逐元素相乘

LeeReamond

2021-11-12 15:41:16 +08:00

@GuuJiang 感谢，所以一般说的矩阵乘法，不是指 element-wise product ，而是指这个 dot ，是按照这个逻辑计算，比如 2*3 矩阵乘 3*2 矩阵得到 2*2 矩阵这样？然后向量的点乘则是指矩阵点乘中的某一步，即按顺序每个位置相乘然后加和，向量的叉乘的话则使用其他逻辑，矩阵不存在叉乘这样？

@qq8331199 这个前几年看过，印象里他主要解释向量计算的物理含义的，看完有收获但是太长时间不用也忘了。而且向量和矩阵关系没搞明白也妨碍我理解

o00O00o

2021-11-13 11:10:15 +08:00

学艺不精，讲讲我的看法。
1. 是可以这样理解的，矩阵由向量组成，行列式对应的则是方阵，因为线代是高度抽象的，在几何中的意义矩阵是代表了线性变换，即代表由一个坐标系变换成为另外一个坐标系过程；而行列式代表变换过程中单位面积被拉伸或缩放的程度。
2. 同#2 说法一样。向量之间的点乘在几何中是一个向量投影到另外一个向量上数量上的乘积。
4. 矩阵相乘上面代码本质上只是算式的计算，你可以在 B 站搜 3Blue1Brown:“线性代数的本质”里面的矩阵的计算方法和我们不太一样，但结果相同。这好比小时候我们学的乘法竖式，我们计算乘法的方法和印度乘法竖式计算方法不同，这我想来应该是从不同的角度来理解。
还是建议多看几遍 B 站上 3Blue1Brown:“线性代数的本质”系列，他是从几何的角度来看，更直观容易理解，我每次看都有新的体会。

zhaofish

2021-11-13 13:47:50 +08:00

问题 1：矩阵是 m*n ，向量是 k 维的，类似 1*k ，如此看来，认为矩阵由向量组成，这个说法没错吧？我还记得上学的时候还有个叫行列式的东西，这个又是什么？
——矩阵可以认为是向量构成的，如果这样理解，矩阵由可以由行向量构成，又可以由列向量构成。在线性代数中，矩阵代表方程组的参数。考虑由以下线性方程组：
a1x + b1y = c1
a2x + b2y = c2
那么 a1, b1, a2, b2 可以组成一个矩阵，称为 A 。

线性代数里，要解决的问题是线性方程组是否有解，线性方程组的解是什么。所以会研究矩阵 A 的性质、操作，其中矩阵的操作包括消元、转置、求逆等。

问题 2：我记得有点乘和叉乘的区别，如下这张图代表的是点乘还是叉乘的计算方法，还是什么其他的别的？
——向量有点乘和叉乘，例如向量 a=[a1 a2], b=[b1 b2]，a 与 b 的点乘= a1*b1 + a2*b2 ，可以看到点乘的结果是一个常数。点乘与叉乘这些内容在解析几何中使用得更多一些。

问题 4：——这个是 numpy 的问题，你可以查看 dot 函数的说明： https://numpy.org/doc/stable/reference/generated/numpy.dot.html 。一维数组的相乘是向量的点乘，二维数组是矩阵乘法，如果是两个常数执行的是常数的乘法。

问题 5：矩阵中挨个位置直接相乘，比如 2*2 矩阵 1,2,3,4 和 5,6,7,8 相乘，得到 5,12,21,32 的话，这种计算规则是叫什么？
—— 这种就是代码中为了计算方便吧，也许有专业的学名，但是不属于线性代数专有的计算。线性代数中定义了矩阵乘法的规则，其中并不包含上面的这种计算法则。

关于线性代数更多的内容，可以看看 MIT 的公开课： https://www.bilibili.com/video/BV1zx411g7gq?p=1