[leetcode/lintcode 题解] 微软面试题：骑士拨号器

[hakunamatata11]

国际象棋中的骑士可以按下图所示进行移动：

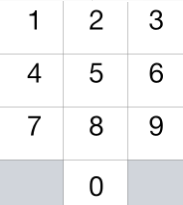
这一次，我们将 “骑士” 放在电话拨号盘的任意数字键（如上图所示）上，接下来，骑士将会跳 N-1 步。每一步必须是从一个数字键跳到另一个数字键。

每当它落在一个键上（包括骑士的初始位置），都会拨出键所对应的数字，总共按下 N 位数字。

你能用这种方式拨出多少个不同的号码？

因为答案可能很大，所以输出答案模 10^9 + 7 。

1≤N≤5000

在线评测地址: https://www.lintcode.com/problem/knight-dialer/?utm_source=sc-v2ex-fks

样例 1：

输入：1
输出：10
说明：
答案可能是 0,1,2,3, ... , 9，

样例 2：

输入：2
输出：20
说明：
答案可能是 04, 06, 16, 18, 27, 29, 34, 38, 43, 49, 40, 61, 67, 60, 72, 76, 81, 83, 94, 92 。

样例 3：

输入：3
输出：46

[题解] 本题采用动态规划的方法，考虑每一步棋子变化的状态，进行统计。我们可以使用滚动数组节省空间。

class Solution {
    public int knightDialer(int N) {
        int MOD = 1_000_000_007;
        int[][] moves = new int[][]{
            {4,6},{6,8},{7,9},{4,8},{3,9,0},
            {},{1,7,0},{2,6},{1,3},{2,4}};

        int[][] dp = new int[2][10];
        Arrays.fill(dp[0], 1);
        for (int hops = 0; hops < N-1; ++hops) {
            Arrays.fill(dp[~hops & 1], 0);
            for (int node = 0; node < 10; ++node)
                for (int nei: moves[node]) {
                    dp[~hops & 1][nei] += dp[hops & 1][node];
                    dp[~hops & 1][nei] %= MOD;
                }
        }

        long ans = 0;
        for (int x: dp[~N & 1])
            ans += x;
        return (int) (ans % MOD);
    }
}

更多语言代码参见：https://www.jiuzhang.com/solution/knight-dialer/?utm_source=sc-v2ex-fks