这是一个创建于 1416 天前的主题,其中的信息可能已经有所发展或是发生改变。
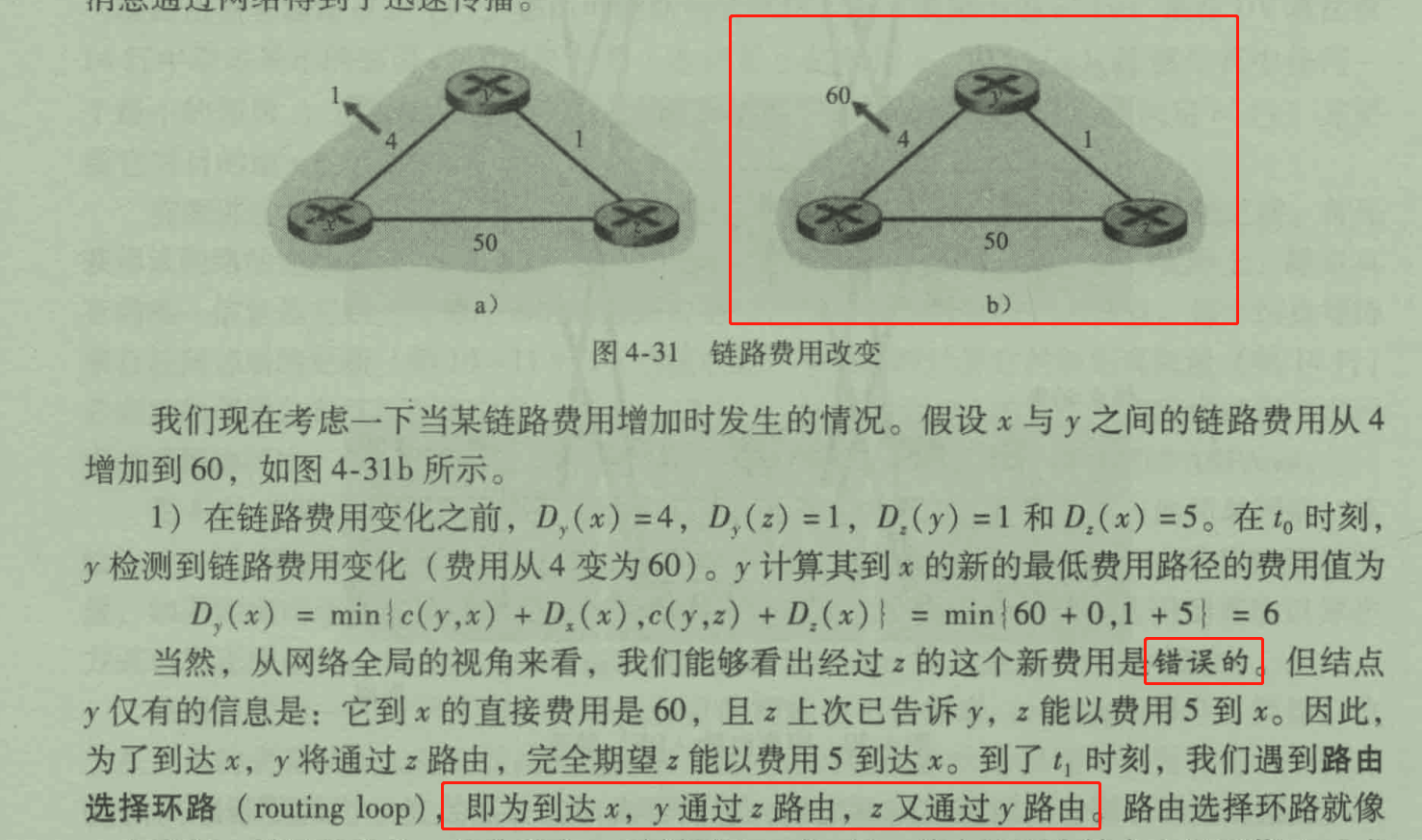 如上这个图,我对照了英文的 pdf ,也是这么写的。然后就有很多疑问。。。
如上这个图,我对照了英文的 pdf ,也是这么写的。然后就有很多疑问。。。
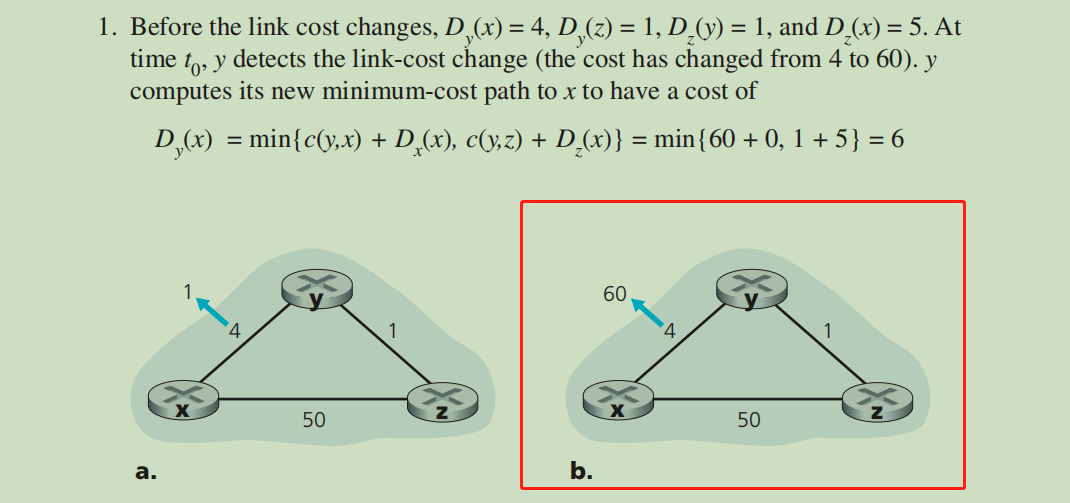 第一:从 x 到 z 的距离在图里明明是 50 ,但原文就是说是 5 ,好,那这里我当是图里的数字错了,其实应该是 5.
第一:从 x 到 z 的距离在图里明明是 50 ,但原文就是说是 5 ,好,那这里我当是图里的数字错了,其实应该是 5.
第二:书里说:“经过 z 的这个新费用是错误的”,但我看就是正确的阿。y 到 x 的话,最小消耗,就是 y => z => x 啊。
第三:z 会更新自己的路由表。所以 Dz(x)=5,即从 z 到 x 的最小消耗是直接从 z 到 x 。所以一个包从 y 到达 z 后,就会直接转到 x 啊,也就不会出现 路由选择环路 了阿?
1
coolan 2021-11-02 21:12:55 +08:00
没仔细看,但是 x-z 最短距离为 4+1
|
2
amiwrong123 OP @coolan #1
嗯,但说的是消耗从 4 变成 60. 的之后的过程 |
3
coolan 2021-11-02 21:30:30 +08:00 我看他写挺明白了,就是由于 4 变为 60 ,z 没更新,导致 y 以为从 z 到 x 是 5 ,然后给 z 发,但是 z 那个 5 的路径是给 y ,这样就回路了。这里你得认为 z 始终没有更新它的路由费用。
|
4
dai201617 2021-11-02 21:45:13 +08:00 楼上老哥解释的挺清楚了。你的第一个问题出发点错了,Dz(x) = Dz(y) +Dy(x) = 4+1 ,所以书上 x 到 z 距离为 50 并没错。这个问题想明白,后面就好理解了
|
5
xiaopc 2021-11-02 21:57:11 +08:00 via iPhone Dz(x) 是 z 通报给 y 的,y 不知道 z 其实是通过自己 (y) 来达到 Dz(x)=5 ,z 也不知道 c(y,x) 改变了
|
6
lmshsqlc 2021-11-03 09:47:53 +08:00 变更前:
y 知道直接去 x 的路只要 4 块 z 知道直接去 y 的路只要 1 块 z 想去 x ,y 告诉他要 4 块,自己的路要 50 块。所以 z 核算成本,走 y 只要 5 块钱,所以 z 记下来了。 所以这时候: y 觉得直接去 x 要 4 块,走 z 要 51 块 z 觉得直接去 x 要 50 块,走 y 要 5 块 那么价格一改: y 发现直接去 x 要 60 块,但是他那边记得走 z 只要 51 z 记得直接去 x 要 50 块,走 y 要 5 块 于是咋的: y 觉得走 z 只要 51 ,就发到 z 去了。 z 觉得走 y 只要 5 块,就发给 y 了。 大概是这么个故事? |
7
2i2Re2PLMaDnghL 2021-11-03 14:21:06 +08:00 c(z,x)=50 没错
因为 z 不知道 c(y,x) 改变了,所以 Dz(x) 错误地被认为是 5 ,实应为 50 所以他们为什么不加撇号,数学推演不加撇号谁知道你改变了 Dy'(x) = min{c'(y,x)+Dx(x), c(y,z)+Dz(x)} = min {60+0,1+5} = 6 理论上来说,每次被请求发送时回传 cost 应该是可以做到趋稳的。 |
8
2i2Re2PLMaDnghL 2021-11-03 14:28:07 +08:00 @2i2Re2PLMaDnghL 没撇全,不过又想起撇号可能和导数混淆?虽然这里不太可能涉及导数,还是标数字
Dy1(x) = min{c1(y,x)+Dx1(x), c1(y,z)+Dz0(x)} = min {60+0,1+5} = 6 当然 Dx1(x) = Dx0(x) 且 c1(y,z) = c0(y,z),所以这两个没问题,然而最后一项还是 Dz0(x) 意思就是 Dz(x) 的根据 t=0 状态计算了。 如果每次回复代价,则会在 45 次沟通后重新趋稳,然而这就是 45 倍风暴了…… 总体代价也颇高。 |
9
amiwrong123 OP 
老哥,再问下,这里之所以叫做无限计数,只是单纯因为从 6 加到>9999 需要很多次吗,所以就叫做 无穷计数吗?或者还是说 跟其他原因有关 @2i2Re2PLMaDnghL #8 |
10
2i2Re2PLMaDnghL 2021-11-05 10:24:13 +08:00 @amiwrong123 看上去是在说随着成本增量的增加,上涨消息传递时间会任意提升。
1e4 需要这么这么多次,那么如果是 1e5 呢? 1e10 呢? 1e20 呢? 所以需要次线性,最好是对数时间复杂度的算法,或者说上涨消息传递时实际上涨应当是超线性甚至是指数性的。 |